En la oportunidad, previo a la realización de un focus group, la directora de Escuela, Dra. Sara Pascual Pizarro, dictó la conferencia sobre “Conocimiento didáctico-matemático que necesita el profesorado para enseñar matemáticas”.
Una provechosa jornada junto a egresados y empleadores realizó la Escuela de Pedagogía en Educación Matemática con el propósito de socializar y recabar impresiones acerca del nuevo perfil de egreso que se propone para el profesor de Matemáticas de la UBB con Mención Didáctica que se describe en los siguientes términos: “El profesor de Educación Matemática de la Universidad del Bío-Bío es un profesional que domina las competencias para conducir el proceso de enseñanza-aprendizaje, comprende los saberes disciplinares de la Matemática y la Didáctica, y los saberes pedagógicos, e integra los valores afectivos y actitudinales con un sello de responsabilidad social, autonomía y espíritu crítico”. El perfil de egreso propuesto pretende recoger en él las necesidades de la sociedad y del mercado laboral.
Sobre dicha definición de interpretación y de competencias específicas tanto Didácticas como Matemáticas, los empleadores y representantes de establecimientos educacionales aportaron sus visiones y valoraciones, considerando la experiencia que han tenido al recibir en sus espacios a estudiantes en práctica y a profesionales egresados de la Escuela de Pedagogía en Educación Matemática de la UBB.
En la oportunidad, la directora de la Escuela de Pedagogía en Educación Matemática, Dra. Sara Pascual Pizarro, dictó la conferencia sobre “Conocimiento didáctico-matemático que necesita el profesorado para enseñar matemáticas”.
La académica ha propuesto que la teoría de las situaciones didácticas procura modelizar la difusión de los conocimientos matemáticos, de una parte para describir el funcionamiento y, por otra parte, para intentar reproducirlo en clase y eventualmente mejorarlo. “¿Pero, cómo saber si hubo completamente y buena difusión, si ha habido desarrollo de conocimientos, si los aprendizajes permitieron la comprensión de los saberes en juego? Podemos desde este momento preguntarnos si es posible saber o conocer sin comprender en matemáticas. Por ejemplo, qué se sabe del teorema de Pitágoras si se produce esto: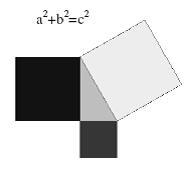
¡No gran cosa! Tal producción, tan emblemática del célebre teorema, no permite concluir que su productor ‘sabe’ el teorema de Pitágoras. Para concluir que alguien sabe, nos proponemos que deba comprender, es decir que sea ‘capaz de reconocer ocasiones de utilizar el saber’ (Brousseau, 1988, p. 49). Por ejemplo, utilizar este teorema para deducir que la hipotenusa necesariamente es el lado más grande del triángulo rectángulo o utilizar otros conocimientos (ex. la similitud o las transformaciones geométricas) para explicar la generalidad y la validez de este teorema”, aseveró la académica.
“Saber, es más que conocer una técnica, un algoritmo o una fórmula. Es también conocer las condiciones de su utilización, es decir saber cuándo utilizarlo y cuando no utilizarlo. Es también poder encontrar nuevas utilizaciones. Saber, es utilizar para recitar (relatar) y calcular absolutos. Pero es también utilizar para resolver, organizar, interrogar y criticar. Todavía es utilizar para probar, validar, invalidar, verificar. Cuando se sabe, podemos también utilizar su saber para jugar, imaginar o inventar. Lo utilizamos también para modelizar, predecir, explicar, sin olvidar para aplicar, decidir, intervenir. Hasta podemos utilizar su saber para integrar otro saber y para abrir a otros aprendizajes”, expresó la Dra. Pascual.
La Directora de la Escuela de Pedagogía en Educación Matemática, Dra. Sara Pascual, destacó que el enfoque por competencias, utilizando la resolución de problemas como marco de desarrollo, propone más bien una nueva pista de respuesta a la pregunta del objetivo de la enseñanza de las matemáticas: “hay que enseñar todo lo que permite el ensanche a corto y largo plazo del campo de problemas resolubles, por el alumno ahora y por el individuo más tarde”, comentó.
